The centripetal acceleration must be
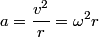 So, 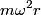 must be the horizontal component of the tension in the cord. The mass is not accelerating in the vertical direction, so the vertical component of the tension must be must be the horizontal component of the tension in the cord. The mass is not accelerating in the vertical direction, so the vertical component of the tension must be 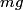 . So, the tension in the cord is: . So, the tension in the cord is: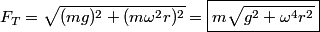 Therefore, answer (E) is correct. |